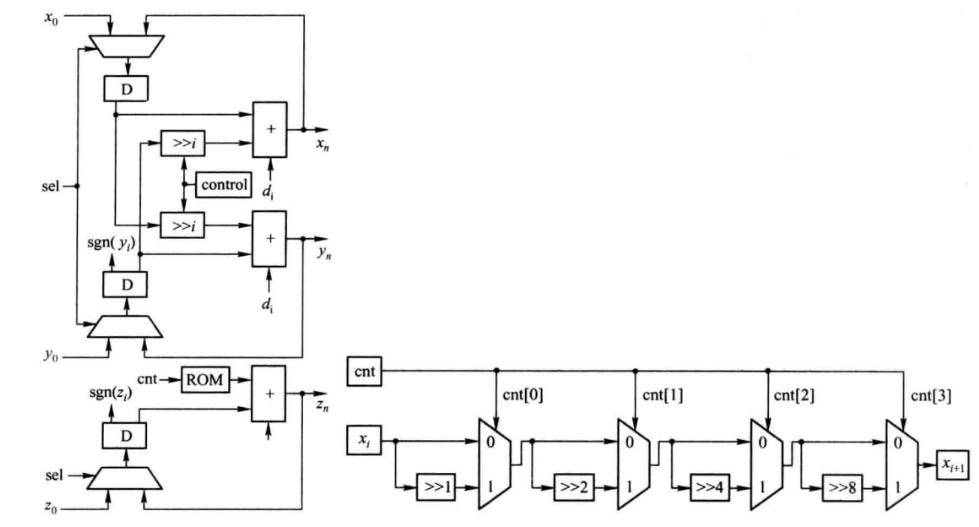
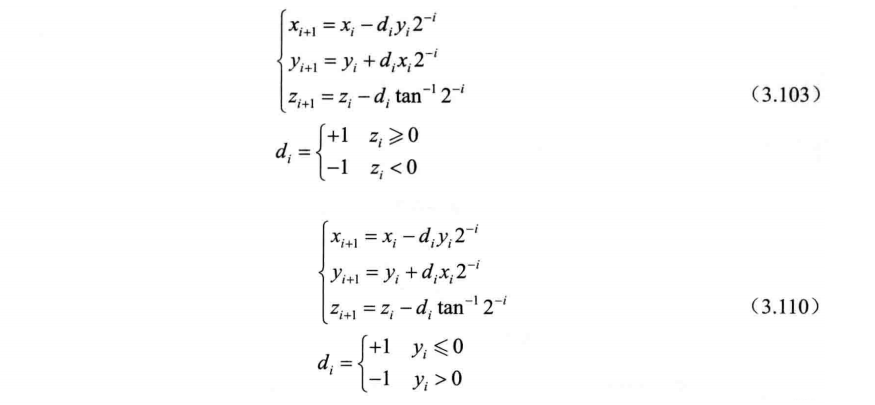Introduction to CORDIC Algorithms
CORDIC (Coordinate Rotation Digital Computer) is a class of iterative algorithms used for efficiently calculating trigonometric, hyperbolic, logarithmic, and exponential functions. Introduced by Jack E. Volder in 1959, CORDIC avoids complex multiplication/division operations by reducing calculations to simple additions, subtractions, and bit shifts, making it ideal for hardware implementations like FPGA-based computers.
Why CORDIC on FPGAs?
Field-Programmable Gate Arrays (FPGAs) are widely used for high-speed and low-power computations due to their parallel processing capabilities and configurability. CORDIC algorithms are well-suited for FPGA implementations because:
- They require minimal hardware resources (no multipliers/dividers).
- They are highly efficient for iterative and pipelined designs.
- They provide accurate results for a variety of mathematical operations.
FPGAs can leverage CORDIC for:
CORDIC Algorithm Overview
The basic CORDIC operation performs rotations in a vector space using iterative angle adjustments. There are two primary CORDIC modes:
- Rotation Mode: Rotates a vector to a target angle.
- Used for trigonometric functions (sine, cosine, magnitude).
- Vectoring Mode: Computes the magnitude and phase (angle) of a vector.
- Used for polar-to-rectangular conversions and vice versa.
The fundamental iterative equations for the CORDIC algorithm are:
Rotation Mode:
xi+1=xi−yi⋅di⋅2−iyi+1=yi+xi⋅di⋅2−izi+1=zi−di⋅arctan(2−i)where di∈{−1,1} is the direction of rotation.
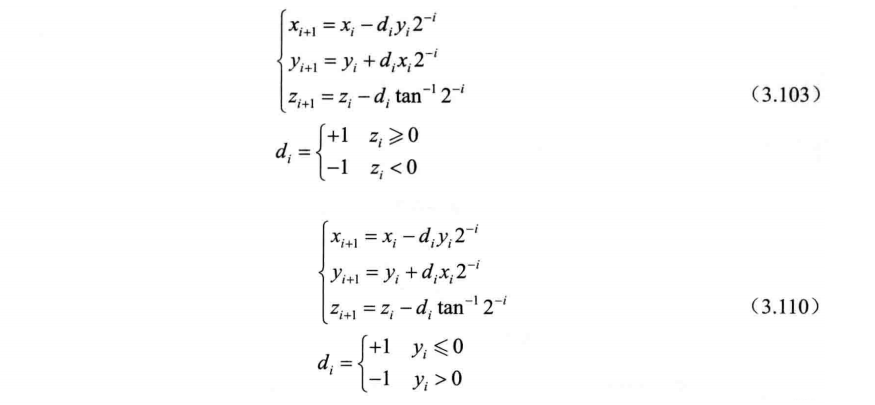
Vectoring Mode: Similar equations are used, but the goal is to nullify the y-component.
Survey of CORDIC Algorithms for FPGA Implementation
Several variations of the CORDIC algorithm exist, each tailored for specific FPGA applications. Below is a summary of the most notable ones:
1. Classical (Basic) CORDIC
- Description: Implements the standard iterative CORDIC algorithm for rotation or vectoring.
- Advantages: Simple architecture; low hardware cost.
- Disadvantages: Slower convergence due to fixed step sizes.
- FPGA Features:
- Requires adders/subtractors and shifters.
- Suited for basic trigonometric computations.
2. Pipelined CORDIC
- Description: The CORDIC iterations are pipelined to achieve higher throughput. Each iteration is implemented in a separate pipeline stage.
- Advantages:
- Extremely high-speed operation; multiple calculations processed in parallel.
- Ideal for real-time applications like DSP and computer graphics.
- Disadvantages: Increased hardware resource usage due to pipeline registers.
- FPGA Features:
- FPGA's parallelism maximizes pipeline efficiency.
- Utilizes multiple clock cycles but with minimum latency.
3. Unrolled CORDIC
- Description: CORDIC iterations are “unrolled” into combinational logic rather than sequential iterations.
- Advantages:
- Faster computation due to elimination of iteration delays.
- Suitable for latency-critical applications.
- Disadvantages:
- Significantly increases area usage on the FPGA.
- May face timing closure challenges for high precision.
4. Iterative CORDIC
- Description: Implements the CORDIC algorithm sequentially, where each iteration occurs in a single clock cycle.
- Advantages:
- Very resource-efficient.
- Suitable for applications with low throughput requirements.
- Disadvantages: Slower compared to pipelined/unrolled versions.
- FPGA Features:
- Minimal use of FPGA logic elements.
5. Hybrid CORDIC
- Description: Combines pipelined and iterative methods to balance resource usage and speed.
- Advantages:
- Optimizes performance while managing hardware costs.
- Disadvantages: Design complexity increases.
- Applications:
- Hybrid designs can adapt to variable precision requirements in FPGA-based computers.
6. Angle Recoding CORDIC
- Description: Uses precomputed tables or recoding techniques to reduce the number of CORDIC iterations.
- Advantages: Faster convergence with fewer iterations.
- Disadvantages: Requires additional memory or precomputed tables.
- FPGA Features:
- Well-suited for modern FPGAs with embedded block RAMs (BRAMs).
Performance Comparison of CORDIC Variants on FPGAs
| Algorithm | Speed | Resource Usage | Applications |
|---|
| Classical CORDIC | Low | Low | Basic trigonometric operations |
| Pipelined CORDIC | High | Moderate/High | Real-time DSP, graphics |
| Unrolled CORDIC | Very High | High | Low-latency, high-throughput systems |
| Iterative CORDIC | Moderate | Very Low | Low-power systems, embedded control |
| Hybrid CORDIC | Moderate/High | Moderate | Precision-critical mixed workloads |
| Angle Recoding CORDIC | High | Moderate | Speed-optimized signal processing |
Applications of CORDIC Algorithms on FPGA-Based Computers
- DSP Systems: FFT, filters, and radar signal processing.
- Computer Vision: Coordinate rotation for image transformations.
- Communication Systems: Phase-locked loops (PLLs), modulation/demodulation.
- Robotics: Real-time inverse kinematics and angle computation.
- Scientific Applications: Logarithmic/exponential function computations.
Challenges in FPGA Implementation of CORDIC
- Precision vs. Speed Trade-Off: Higher precision requires more iterations and resources.
- Resource Utilization: Pipelined and unrolled CORDIC designs consume significant FPGA resources.
- Power Efficiency: Iterative designs are more power-efficient but slower.
- Timing Closure: High-speed designs may face routing delays on large FPGAs.
Conclusion
The CORDIC algorithm remains a popular choice for FPGA-based computers due to its simplicity, resource efficiency, and versatility. Variants like pipelined CORDIC, unrolled CORDIC, and angle recoding CORDIC offer trade-offs in speed, resource usage, and complexity. By selecting the appropriate variant and optimization techniques, FPGA-based systems can achieve efficient real-time mathematical computations for diverse applications.